最佳止步问题(optimal stopping)[2]
最佳的选择:
首先我们先规定几个标记,以方便论证:
![\[x_{k}\] \[x_{k}\]](/user_files/SPECODER/epics/0318b5382a48a5052b3125eea904dac342fb5c59.png) :表示第 k 个物品的名次,即实际名次。显然,这是个随见变量,而且我们对于该名次,之前是一无所知的,但是我们知道的,是每个物品的临时名次,也就是说,当我们看到第 k 个物品时,该物品在前 k 个物品中排第几我们是知道的。
:表示第 k 个物品的名次,即实际名次。显然,这是个随见变量,而且我们对于该名次,之前是一无所知的,但是我们知道的,是每个物品的临时名次,也就是说,当我们看到第 k 个物品时,该物品在前 k 个物品中排第几我们是知道的。
前面简单的办法,即放弃前面一半,结果已经十分不错了,我们自然会想到跟一般的办法。
![\[M_{r}\] \[M_{r}\]](/user_files/SPECODER/epics/89c6fb8bba859f8cba7612adac85b4404325dc24.png) : 放弃前面 k-1 位。自第 r 位起,首次遇到较前均佳者即停。
: 放弃前面 k-1 位。自第 r 位起,首次遇到较前均佳者即停。
也就是说,自第 r 位起,选择首次出现的临时第一名。请注意,所谓放弃前面 r-1 位,当然是你决不选他们,但是你仍应对这些物品打量一番,以便与后来的作个比较,也就是说,以便决定后来者的临时名次。又 M1,没有什么意思:你必须选取第一位,因为第一位一定是一个临时第一名。
![\[P(M_{r})\] \[P(M_{r})\]](/user_files/SPECODER/epics/b4f0a6550e2999264703af9e28d5fdcba5221fff.png) 为根据上述办法,选中第一名的机率
为根据上述办法,选中第一名的机率
Sk为根据上述办法,第k件物品被选的事件
则,可得:
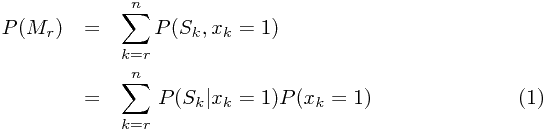
这里![\[P(A,B)\] \[P(A,B)\]](/user_files/SPECODER/epics/7c1308fe1fc209257281321cc048bc686ebb879d.png) 代表
代表![\[P(AB)\] \[P(AB)\]](/user_files/SPECODER/epics/1d796050c5d9195873944e4da6525d20bdf5fce5.png) ,即A和B同时发生的概率。
,即A和B同时发生的概率。
好的,让我们一步一步地阐明这个公式的意义,
首先,我们利用![\[M_{r}\] \[M_{r}\]](/user_files/SPECODER/epics/89c6fb8bba859f8cba7612adac85b4404325dc24.png) 这个策略,要获胜,只有可能是取了再
这个策略,要获胜,只有可能是取了再![\[[k,n]\] \[[k,n]\]](/user_files/SPECODER/epics/e12b6b670d7c189d7f0d68b3e34d72b7fdc5bcce.png) 中选取了一个,且我们取得的物品(第 k 个物品)一定要是实际排名第一位的物品。
中选取了一个,且我们取得的物品(第 k 个物品)一定要是实际排名第一位的物品。
这个事件有可能发生在![\[[k,n]\] \[[k,n]\]](/user_files/SPECODER/epics/e12b6b670d7c189d7f0d68b3e34d72b7fdc5bcce.png) 中的任何一个物品上面,所以这 n-k+1 个随机事件中只要有一个发生(即为真),
中的任何一个物品上面,所以这 n-k+1 个随机事件中只要有一个发生(即为真),![\[M_{r}\] \[M_{r}\]](/user_files/SPECODER/epics/89c6fb8bba859f8cba7612adac85b4404325dc24.png) 则为真。
则为真。
所以这 n-k+1 个事件之间是“或”的关系,所以,这里我们用求和。之后的就很好理解了,
![\[P(S_k,x_k=1)=\,P(S_k\vert x_k=1)P( x_k=1)\] \[P(S_k,x_k=1)=\,P(S_k\vert x_k=1)P( x_k=1)\]](/user_files/SPECODER/epics/ce75e7d4d465d3c89df91bed3b1ae7676294df77.png)
这是利用条件概率的公式:![\[P(AB)=\,P(A\vert B)P(B)=\,P(B\vert A)P(A)\] \[P(AB)=\,P(A\vert B)P(B)=\,P(B\vert A)P(A)\]](/user_files/SPECODER/epics/c068f56aff23a77071940413a9cafda8bcfe99a7.png) ,这在任何一本概率统计的书都会讲到。意义也很好理解:
,这在任何一本概率统计的书都会讲到。意义也很好理解:
即 A 事件与 B 事件要同时发生的概率 等于 在 A 事件发生的情况下 B 也发生 且同时 A 也发生的这个事件的概率,注意是同时发生,所以 P(A|B)和P(B) 之间是相乘的关系,A,B 位置反之亦然。
显然,![\[P( x_k=1)=\frac{1}{n} \] \[P( x_k=1)=\frac{1}{n} \]](/user_files/SPECODER/epics/e6ff62f01cd93e58b041cf5cddc0ee7be0fec488.png)
那么,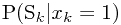 又等于什么呢?
又等于什么呢?
我们可以这么看,假如第一名在第 k 个位置,那么,按照,只![\[M_{r}\] \[M_{r}\]](/user_files/SPECODER/epics/89c6fb8bba859f8cba7612adac85b4404325dc24.png) 有下面的情形我们才能选到它:
有下面的情形我们才能选到它:
前面k-1个物品中的最好的物品(不是实际的最好)要发生在最前面r-1个位置里。
这里为了方便表述,这个情形,记作:事件N。
这个很好理解,因为如果不是这样,即前面 k-1 个物品中的最好的物品在![\[[r,k-1]\] \[[r,k-1]\]](/user_files/SPECODER/epics/da99224764cca7dbc463dacd374d3578afe4fa1d.png) 这个区间中,那么必然会在检查第k件物品之前就做出了选择,拿走了物品,不可能检查得到 k 个物品。所以,以上的这个事件N是: 在
这个区间中,那么必然会在检查第k件物品之前就做出了选择,拿走了物品,不可能检查得到 k 个物品。所以,以上的这个事件N是: 在![\[ x_k=1\] \[ x_k=1\]](/user_files/SPECODER/epics/cf252e698ef48bd110efa5aab797f3cf48b37dc9.png) 的条件下,
的条件下,![\[ S_k\] \[ S_k\]](/user_files/SPECODER/epics/492ee5ac23953b4e5213a43abb6cf3a8b9093838.png) 发生的必要条件,即:
发生的必要条件,即:
在![\[ x_k=1\] \[ x_k=1\]](/user_files/SPECODER/epics/cf252e698ef48bd110efa5aab797f3cf48b37dc9.png) 的成立的条件下,
的成立的条件下,![\[ S_k\] \[ S_k\]](/user_files/SPECODER/epics/492ee5ac23953b4e5213a43abb6cf3a8b9093838.png) 发生
发生 ![\[ \Longrightarrow\] \[ \Longrightarrow\]](/user_files/SPECODER/epics/c57e64e09d7884992fcdb3ceb360fb226fa752dd.png) 事件N 发生。反过来,如果在
事件N 发生。反过来,如果在![\[ x_k=1\] \[ x_k=1\]](/user_files/SPECODER/epics/cf252e698ef48bd110efa5aab797f3cf48b37dc9.png) 的条件下,事件N 发生,那么我们也必然会做出 取走第k个的选择,即,
的条件下,事件N 发生,那么我们也必然会做出 取走第k个的选择,即,![\[ S_k\] \[ S_k\]](/user_files/SPECODER/epics/492ee5ac23953b4e5213a43abb6cf3a8b9093838.png) 发生。
发生。
可知: 如果在![\[ x_k=1\] \[ x_k=1\]](/user_files/SPECODER/epics/cf252e698ef48bd110efa5aab797f3cf48b37dc9.png) 的条件下,
的条件下,![\[ S_k\] \[ S_k\]](/user_files/SPECODER/epics/492ee5ac23953b4e5213a43abb6cf3a8b9093838.png) 发生
发生 ![\[ \Longleftrightarrow\] \[ \Longleftrightarrow\]](/user_files/SPECODER/epics/bed25287b46a73e480c14fe08550742f142b9723.png) 事件N 发生。所以,在
事件N 发生。所以,在![\[ x_k=1\] \[ x_k=1\]](/user_files/SPECODER/epics/cf252e698ef48bd110efa5aab797f3cf48b37dc9.png) 的条件下,
的条件下,![\[ S_k\] \[ S_k\]](/user_files/SPECODER/epics/492ee5ac23953b4e5213a43abb6cf3a8b9093838.png) 与事件N 是等价的事件。
与事件N 是等价的事件。
综上所述,![\[\,P(S_k\vert x_k=1)=\frac{r-1}{k-1}\] \[\,P(S_k\vert x_k=1)=\frac{r-1}{k-1}\]](/user_files/SPECODER/epics/3163bdc4e37ef78271c9f44bfe29e6609d63ebb4.png)
因此,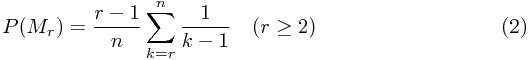
显然,![\[P(M_{1})=1/n\] \[P(M_{1})=1/n\]](/user_files/SPECODER/epics/a77ec3f75afc2af974b3b95b33233d09c5cda466.png) ,
,
同时,(2)式是个仅仅与 r 有关的函数,可以记作:![\[f(r)\] \[f(r)\]](/user_files/SPECODER/epics/e8cb93a142cf63ffeb43b6166af60a48c20fbdd2.png) ,而我们要求的便是一个
,而我们要求的便是一个 ![\[r^{*}\] \[r^{*}\]](/user_files/SPECODER/epics/137ee876318a1d4c3e71e82552d63ca3f90658db.png) 使得
使得![\[f(r)\] \[f(r)\]](/user_files/SPECODER/epics/e8cb93a142cf63ffeb43b6166af60a48c20fbdd2.png) 取得到最大值
取得到最大值![\[f(r^{*})\] \[f(r^{*})\]](/user_files/SPECODER/epics/694f750a49209cf21392fa37d455f07c1c2bc679.png) ,那么,
,那么,![\[M_{r^{*}}\] \[M_{r^{*}}\]](/user_files/SPECODER/epics/f807093c480df270828b34ab2bc601f30031c925.png) 就是最佳的选择方法。看到这里,比较细心一点的读者也许会问:你怎么可以保证没有再好的办法呢?换句话说:最好的办法,一定是在上述这类
就是最佳的选择方法。看到这里,比较细心一点的读者也许会问:你怎么可以保证没有再好的办法呢?换句话说:最好的办法,一定是在上述这类![\[(M_r:r=2,3\cdots)$\] \[(M_r:r=2,3\cdots)$\]](/user_files/SPECODER/epics/54dab37595790e27d9ec5f6860e7325512f4662e.png) 里面吗?答案是肯定的,证明也不是很难;等我以后时间,会在blog上给出证明。读者如要深究,可参照资料下篇文章文末的参看数目中的[4][5],好好想一想。
里面吗?答案是肯定的,证明也不是很难;等我以后时间,会在blog上给出证明。读者如要深究,可参照资料下篇文章文末的参看数目中的[4][5],好好想一想。
接下来,以 ![\[\triangle f(r)=f(r+1)-f(r)\] \[\triangle f(r)=f(r+1)-f(r)\]](/user_files/SPECODER/epics/6f403f39f870436e52e1221b6f17dae22a91e554.png) 代表
代表![\[f(r)\] \[f(r)\]](/user_files/SPECODER/epics/e8cb93a142cf63ffeb43b6166af60a48c20fbdd2.png) 的“增率”。即,
的“增率”。即,![\[f(r)\] \[f(r)\]](/user_files/SPECODER/epics/e8cb93a142cf63ffeb43b6166af60a48c20fbdd2.png) 的差分。
的差分。
从(2)式我们可以看到:
![\setcounter{equation}{2}\begin{eqnarray}\triangle f(r)&=&\frac{r}{n}(\frac{1}{r}+{}\cdots+\frac{1}{n-1})-\frac{r-1}{n}(\frac{1}{r-1}+\frac{1}{r}+{}\cdots+\frac{1}{n-1})\nonumber\\ {}&=&\frac{1}{n}\Big[r(\frac{1}{r}+\cdots+\frac{1}{n-1})-1-(r-1)(\frac{1}{r}+\cdots+\frac{1}{n-1})\Big]\nonumber\\ {}&=&\frac{1}{n}(-1+\displaystyle\sum_{k=r}^{n-1}\frac{1}{k})\\ \end{eqnarrqy} \setcounter{equation}{2}\begin{eqnarray}\triangle f(r)&=&\frac{r}{n}(\frac{1}{r}+{}\cdots+\frac{1}{n-1})-\frac{r-1}{n}(\frac{1}{r-1}+\frac{1}{r}+{}\cdots+\frac{1}{n-1})\nonumber\\ {}&=&\frac{1}{n}\Big[r(\frac{1}{r}+\cdots+\frac{1}{n-1})-1-(r-1)(\frac{1}{r}+\cdots+\frac{1}{n-1})\Big]\nonumber\\ {}&=&\frac{1}{n}(-1+\displaystyle\sum_{k=r}^{n-1}\frac{1}{k})\\ \end{eqnarrqy}](/user_files/SPECODER/epics/a4f3a2bb7577a4a6225959d001ba9d1c34be2e65.png)
此处,n 为定值,若 r 增加,则,求和的项数减少,而每项又都是正的,由此可知,![\[\triangle f(r)\] \[\triangle f(r)\]](/user_files/SPECODER/epics/5865cad1be24b639e57d86bd62a78712095108d8.png) 是r的单调减函数。
是r的单调减函数。
同时,![\[\triangle f(r)\] \[\triangle f(r)\]](/user_files/SPECODER/epics/5865cad1be24b639e57d86bd62a78712095108d8.png) 的初始值,即 r=2 时,可以取得到最大值,
的初始值,即 r=2 时,可以取得到最大值,
![\[\[\triangle f(2)=\frac{1}{n}(-1+\frac{1}{2}+\cdots+\frac{1}{n-1})\]\] \[\[\triangle f(2)=\frac{1}{n}(-1+\frac{1}{2}+\cdots+\frac{1}{n-1})\]\]](/user_files/SPECODER/epics/02c375c5fe584e4a214f7582a23792d95a96940f.png) , 该式在
, 该式在 ![\[n \ge 5\] \[n \ge 5\]](/user_files/SPECODER/epics/7cc19dc719a9f69aaf9a314e9c678ac694b75aa0.png) 的时候为正数,其实,我们可以发现,当n不大的时候,用这样的策略的意义并不是很大,因为即使是随机地去,概率:1/n 也会很大,所以在此不妨设 n 的范围是
的时候为正数,其实,我们可以发现,当n不大的时候,用这样的策略的意义并不是很大,因为即使是随机地去,概率:1/n 也会很大,所以在此不妨设 n 的范围是 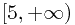 , 继而,我们可以论证
, 继而,我们可以论证 ![\[n < 5\] \[n < 5\]](/user_files/SPECODER/epics/bb6e8d10864193d65a725b19a430c5ae1f95c2ab.png) 的情况(利用(2)式):
的情况(利用(2)式):
n=1: 只有一个可选,不得不选第一个。
n=2:![\[P(M_{r})_{max}=P(M_{1})=P(M_{2})=1/2\] \[P(M_{r})_{max}=P(M_{1})=P(M_{2})=1/2\]](/user_files/SPECODER/epics/0446fb817c5c35dd80b7296285ae0d191e194ee1.png)
n=3: ![\[P(M_{r})_{max}=P(M_{2})=1/2\] \[P(M_{r})_{max}=P(M_{2})=11/24\]](/user_files/SPECODER/epics/cdd91c24e3f3bafde63cf2d4cfd07e6cb87cf249.png)
n=4: ![\[P(M_{r})_{max}=P(M_{2})=11/24\] \[P(M_{r})_{max}=P(M_{2})=11/24\]](/user_files/SPECODER/epics/cb4362cd7399ad9fe9f57c70e05e32deddecaa01.png)
之后对于,![\[n \ge 5\] \[n \ge 5\]](/user_files/SPECODER/epics/7cc19dc719a9f69aaf9a314e9c678ac694b75aa0.png) 的情况的分析如下,
的情况的分析如下,
![\[\triangle f(2) > 0\] \[\triangle f(2) > 0\]](/user_files/SPECODER/epics/2cf403c8c52039b6157bfce7879453340f6c9e0c.png) 而
而 ![\[\triangle f(n-1) =\frac{1}{n}(-1+\frac{1}{n-1})} < 0\] \[\triangle f(n-1) =\frac{1}{n}(-1+\frac{1}{n-1})} < 0\]](/user_files/SPECODER/epics/da949f3a39799cf9c43b2a0965f21968c7bb020a.png)
所以在 ![\[[ 5, n-1 ]\] \[[ 5, n-1 ]\]](/user_files/SPECODER/epics/3ae5159b1968bcd8c1dff7decae940e6368ce792.png) 的定义区间内,必定存在一点
的定义区间内,必定存在一点 ![\[r^*\] \[r^*\]](/user_files/SPECODER/epics/df22aa319cd7b432aff4cb27733b3084000b6303.png) 使得
使得![\[\triangle f(r)\] \[\triangle f(r)\]](/user_files/SPECODER/epics/5865cad1be24b639e57d86bd62a78712095108d8.png) 最接近0(可能大于0,也可能等于0,不能是小于0),同时也使得
最接近0(可能大于0,也可能等于0,不能是小于0),同时也使得![\[f(r)\] \[f(r)\]](/user_files/SPECODER/epics/e8cb93a142cf63ffeb43b6166af60a48c20fbdd2.png) ,即
,即![\[P(M_{r})\] \[P(M_{r})\]](/user_files/SPECODER/epics/b4f0a6550e2999264703af9e28d5fdcba5221fff.png) 取得最大值。
取得最大值。
如,图(1)(此处 n=12)

所以就有, ![\[\sum^{n-1}_{r^*}\,(\frac{1}{k})-1\leq 0\] \[\sum^{n-1}_{r^*}\,(\frac{1}{k})-1\leq 0\]](/user_files/SPECODER/epics/459f5c9d07871817e7b5ec2102e611347398b622.png) 且
且 ![\[\sum^{n-1}_{r^*-1}(\frac{1}{k})-1>0\] \[\sum^{n-1}_{r^*-1}(\frac{1}{k})-1>0\]](/user_files/SPECODER/epics/af656fcc2cf2631f8801cee8a4dbaf226ac98c8f.png) ,即:
,即:
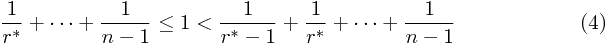
任意定了n后,![\[r^*\] \[r^*\]](/user_files/SPECODER/epics/df22aa319cd7b432aff4cb27733b3084000b6303.png) 就可自(4)式中计算出来。
就可自(4)式中计算出来。
这里有趣的是,虽然![\[r^*\] \[r^*\]](/user_files/SPECODER/epics/df22aa319cd7b432aff4cb27733b3084000b6303.png) 随n而变,但当 n 很大时,
随n而变,但当 n 很大时,![\[\frac{r^*}{n}\] \[\frac{r^*}{n}\]](/user_files/SPECODER/epics/079c5067efdfc2ae7878fd37dc22b2216db4810d.png) 几乎没有什么变化。(事实上,实际的数据显示,n =20已经可算“很大”了)。怎样看出这点来?这里我们要提到“自然对数”
几乎没有什么变化。(事实上,实际的数据显示,n =20已经可算“很大”了)。怎样看出这点来?这里我们要提到“自然对数”![\[\log\] \[\log\]](/user_files/SPECODER/epics/afe031de081d33ff35796514f8c3f0841e597be4.png) 。这是以
。这是以![\[e \approx 2.718\] \[e \approx 2.718\]](/user_files/SPECODER/epics/59bfc83b6825b4cf5c761094eacd1ccd2b0a7db0.png) 为底的对数函数。(有人将这
为底的对数函数。(有人将这![\[\log\] \[\log\]](/user_files/SPECODER/epics/afe031de081d33ff35796514f8c3f0841e597be4.png) 写作
写作![\[\log_{e}\] \[\log_{e}\]](/user_files/SPECODER/epics/0662f58e1c2a9643fbfca03a9ea7bbda49e21f07.png) 或者
或者![\[\ln\] \[\ln\]](/user_files/SPECODER/epics/b6a4d3da942ce0abf0e4ec2b5de6ddaea37ea32f.png) )。它是怎样来的?最好的定义方法是:
)。它是怎样来的?最好的定义方法是: ![\[\ln t\] \[\ln t\]](/user_files/SPECODER/epics/34666b5b68849ce1b96d6cb9f73cbcdf8b994f34.png) 是曲线
是曲线![\[y=\frac{1}{x}\] \[y=\frac{1}{x}\]](/user_files/SPECODER/epics/e8e428c109808c65a61583de836d63fdda30c9c2.png) 与 x 轴在
与 x 轴在 ![\[x=1\] \[x=1\]](/user_files/SPECODER/epics/bd1f3b79821ba2f3ff0990874add3fef21061476.png) 和
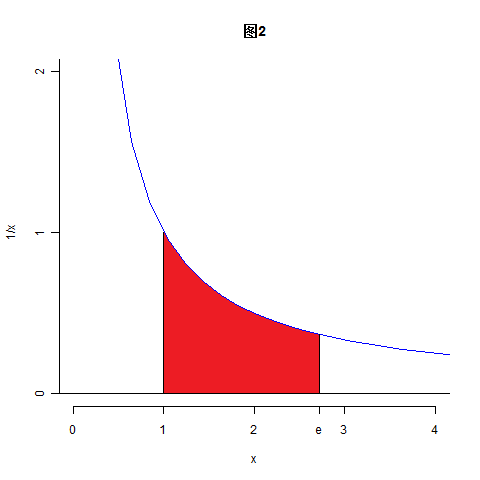
和 ![\[x=t\] \[x=t\]](/user_files/SPECODER/epics/8725c4752bd7f8e53d4dda0a928bb2c10585ad02.png) 之间的面积,如图(2)。这样说的话,
之间的面积,如图(2)。这样说的话,![\[e\] \[e\]](/user_files/SPECODER/epics/bf37cd38183da25140a40def1d15780fa08ac181.png) 就是
就是![\[\ln t =1\] \[\ln t =1\]](/user_files/SPECODER/epics/4ed1b51496989514b1ec7f63eaa6bf3a4aa75171.png) 的唯一的实数解。图中红色部分的面积为 1.
的唯一的实数解。图中红色部分的面积为 1.
接下来,让我们继续看两幅图,


由(图3)可知,所有矩形的面积和:![\[1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n-1} > \ln(n)\] \[1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n-1} > \ln(n)\]](/user_files/SPECODER/epics/9fcaf6e045ae8387ed6a7a6cde177937e58a2859.png)
而由(图4)可知,所有矩形的面积和:![\[\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n} < \ln(n)\] \[\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n} < \ln(n)\]](/user_files/SPECODER/epics/1d7472f97c61a0f8788c278242651714c5dae4aa.png)
经过简单的移项,可得: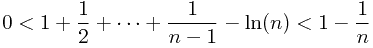
所以,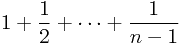 与
与 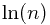 的差在
的差在 ![\[[ 0, 1 ]\] \[[ 0, 1 ]\]](/user_files/SPECODER/epics/a786de717e5b7bd0ff472b7da974dc86564271f6.png) 之间,最多不过差1.
之间,最多不过差1.
事实上当n增加时, ![\[1+\frac{1}{2}+\cdots+\frac{1}{n-1}-\ln(n)\] \[1+\frac{1}{2}+\cdots+\frac{1}{n-1}-\ln(n)\]](/user_files/SPECODER/epics/adf6f8ed9c5d1f64099960c325b4f29e0a6a5729.png) 会有一个极限,这个极限叫做欧拉(Euler)常数,其值约为0.5772,即:
会有一个极限,这个极限叫做欧拉(Euler)常数,其值约为0.5772,即:
![\[\lim_{n \rightarrow +\infty}\Big[ 1+\frac{1}{2}+\cdots+\frac{1}{n-1}-\ln(n) \Big] \approx 0.5772 \] \[\lim_{n \rightarrow +\infty}\Big[ 1+\frac{1}{2}+\cdots+\frac{1}{n-1}-\ln(n) \Big] \approx 0.5772 \]](/user_files/SPECODER/epics/11e9ac2919f8bdad27131f3a463b1ad7437d16de.png)
关于欧拉常数的证明,稍后会出现在blog上,有情趣的看管,可以前去查看。
所以,可以合理的做出假设:
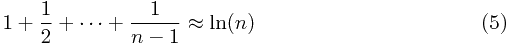
根据式(5):![\[\frac{1}{r^*}+\cdots+\frac{1}{(n-1)}\approx\ln{n}-\ln{r^*}=\ln{(\frac{n }{r^*})}\] \[\frac{1}{r^*}+\cdots+\frac{1}{(n-1)}\approx\ln{n}-\ln{r^*}=\ln{(\frac{n }{r^*})}\]](/user_files/SPECODER/epics/3b0017d22598be2bc66cb7b8acd1295f690668a8.png)
当 n 很大时,(4)式中左右两边相差无几,(两边相差只一项。请注意(4)式的左边显示,当 n 很大时,r * 也必很大,否则左面就会超过1 ), 因此(4 )式可以大约写为:
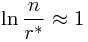
因为![]() ,所以
,所以
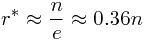
这时,![\[f(r^*)\] \[f(r^*)\]](/user_files/SPECODER/epics/e1c6d27ec0dbab4411a1950461b1586704f4a67e.png) 大约是
大约是
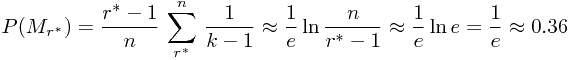
所以,使用![\[M_{0.36n}\] \[M_{0.36n}\]](/user_files/SPECODER/epics/ab0fb398781b90aa35c2b1bde016fe5cc9b0b2ee.png) 该策略使得我们有近 0.36 的几率选到第一名。当n很大时,该策略的优越性不言而喻。
该策略使得我们有近 0.36 的几率选到第一名。当n很大时,该策略的优越性不言而喻。
其实在计算![\[r^*\] \[r^*\]](/user_files/SPECODER/epics/df22aa319cd7b432aff4cb27733b3084000b6303.png) 的时候,也可以利用,化离散为连续的思想,当然需要一点技巧和高等数学的基础。
的时候,也可以利用,化离散为连续的思想,当然需要一点技巧和高等数学的基础。
现在,我们令:![\[x=\frac{r}{n}\] \[x=\frac{r}{n}\]](/user_files/SPECODER/epics/fd554d811f7453800e24fdca59b1b74b07b9a6cb.png) (且此时,n 和
(且此时,n 和 ![\[r^*\] \[r^*\]](/user_files/SPECODER/epics/df22aa319cd7b432aff4cb27733b3084000b6303.png) 都很大),则(2)式可化为
都很大),则(2)式可化为 ![\[f(x)=x \ln(1/x)\] \[f(x)=x \ln(1/x)\]](/user_files/SPECODER/epics/d9653cc8f03585ae521c1b7b1a92a2a775ba430e.png) , 令
, 令![\[f^\prime(x)=0\] \[f^\prime(x)=0\]](/user_files/SPECODER/epics/e4884962944d64704e7406ec87d70b2e73db8d2b.png) ,可得:
,可得:![\[x^*=1/e\] \[x^*=1/e\]](/user_files/SPECODER/epics/d508fb96e5e0552c5689a6c039e256676e5ead61.png) ,而由
,而由![\[\begin{array}{lr}f^{\prime\prime}(x)=-\frac{1}{x}-1 < 0 & (x > 0)\end{array}\] \[\begin{array}{lr}f^{\prime\prime}(x)=-\frac{1}{x}-1 < 0 & (x > 0)\end{array}\]](/user_files/SPECODER/epics/b06dcd80c41ca7f8a0f26c3c3ec59f3a41cf9add.png) 可知,
可知,![\[f(x)\] \[f(x)\]](/user_files/SPECODER/epics/989d95e42b00edcf853fe9fff41d0fba80e8a9a8.png) 在
在![\[x^*=1/e\] \[x^*=1/e\]](/user_files/SPECODER/epics/d508fb96e5e0552c5689a6c039e256676e5ead61.png) 这一点上取到最大值,即,当
这一点上取到最大值,即,当 ![\[\frac{r^*}{n}=\frac{1}{e}\] \[\frac{r^*}{n}=\frac{1}{e}\]](/user_files/SPECODER/epics/35b5860c04c911582ec5f276ff8038e02227a515.png) 时,
时,![\[f(r)\] \[f(r)\]](/user_files/SPECODER/epics/e8cb93a142cf63ffeb43b6166af60a48c20fbdd2.png) 取得到最大值,此时,
取得到最大值,此时,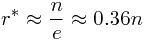 ,于之前得出的结论相同。
,于之前得出的结论相同。
特别说明:
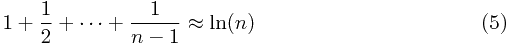
根据式(5):![\[\frac{1}{r^*}+\cdots+\frac{1}{(n-1)}\approx\ln{n}-\ln{r^*}=\ln{(\frac{n }{r^*})}\] \[\frac{1}{r^*}+\cdots+\frac{1}{(n-1)}\approx\ln{n}-\ln{r^*}=\ln{(\frac{n }{r^*})}\]](/user_files/SPECODER/epics/3b0017d22598be2bc66cb7b8acd1295f690668a8.png)
也许很多人会对上式中“约等于”的准确性有所疑问,但是事实是,上式用了两次(5)式的近似,当 n 和 r* 很大的时候,(5)式左右两边的差十分趋向于欧拉常数,导致在对于两次近似的误差做减法的时候完全可以把这两个误差的差值视作为0.而对于 n 和 r* 都比较小的情况下,误差也许会很大,但是绝对是在可以接受的范围之内的,因为根据上面所说,在n很小时候,不是很能体现这种策略的优越性,因为和直接随机取得第一名的概率相差也不是很大。即使有误差,也不会离最佳策略的概率差很多。反过来说,当 n 很大时,我们用该策能很好的提高优越性之外,准确性也大幅提高。而准确性的提高又使得我们更佳地接近最终被优化的概率。希望下面的几幅图能给读者一个更形象的认识:

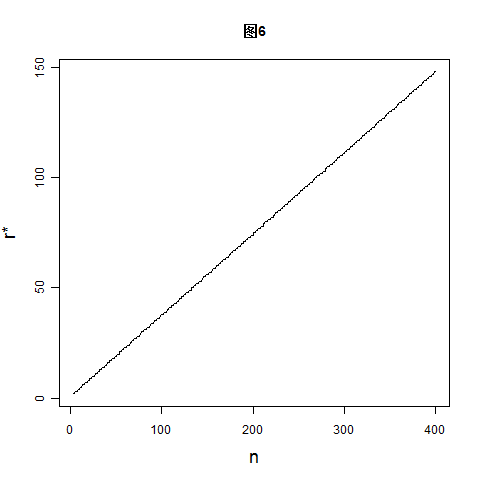

图(5)中,y轴上的 r* 是精确值,而不是估算值,可以看到,当 n 很大时,![\[\frac{r*}{n}\rightarrow 1/e\] \[\frac{r*}{n}\rightarrow 1/e\]](/user_files/SPECODER/epics/c81b5081ae3de32acd40c609a803753993c75a91.png)
图(6)是精确的 r* 与 n 的关系,可以看出,近似于一条斜率为 0.36 的直线。
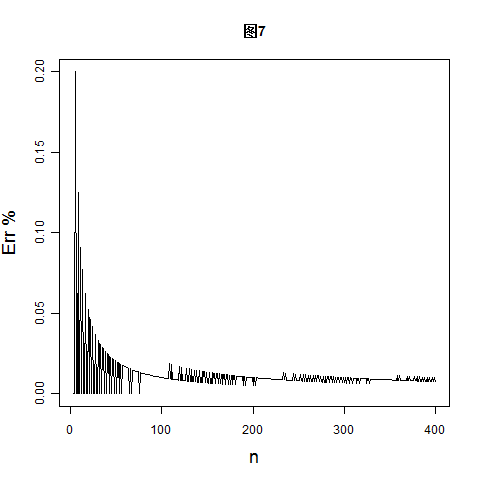
图(7),是百分比误差与 n 的关系,可以明显看出,百分比误差随 n 的增大急剧减小。
图(8),是由在估算 r* 时造成误差引起概率的误差 与 n 的关系,同样可以看出,百误差随 n 的增大急剧减小。
至此,我们得出了一个比较优化的策略,使得我们取到第一名的概率提高了很多,但是,如果我们退而求其次,即,如果,我们取到实际的第一名或者第二名也满足胜利条件的,我们又会用什么更好的策略呢?如果存在这种策略,届时取到第一或第二的概率又会是多少呢?
(未完待续……)
May 02, 2022 11:01:53 PM
It’s actually a nice and useful piece of info. I am happy that you just shared this helpful information with us. Please keep us up to date like this. Thanks for sharing. How to Sell Credit Card Processing
====================================================================
Excellent website you have here but I was curious if you knew of any message boards that cover the same topics talked about in this article? I’d really love to be a part of group where I can get advice from other knowledgeable people that share the same interest. If you have any recommendations, please let me know. Cheers! Merchant Service Commission
Jul 21, 2022 03:22:45 PM
Thanks for every other excellent post. The place else may just anyone get that kind of info in such an ideal manner of writing? I’ve a presentation subsequent week, and I am at the look for such information. 雲台
Aug 24, 2022 01:31:45 PM
Amazingly, your piece goes to the heart of the topic. Your clarity leaves me wanting to know more. Just so you know, i’ll immediately grab your feed to keep up currently with your online blog. Sounding Out thanks is merely my little way of claiming what a masterpiece for a fantastic resource. Take On my best wishes for your subsequent publish. acne
Aug 24, 2022 05:38:59 PM
Nice post! This really is a very nice blog that I will definitively return to more times this year! Thanks for informative post. 오피스타
Oct 10, 2023 05:48:19 PM
Great job for publishing such a beneficial web site. Your web log isn’t only useful but it is additionally really creative too. <a href="https://linktr.ee/ReubenGloverJr">Easy1Up Review</a>