最佳止步问题(optimal stopping)[3]
退而求其次:
如果你把眼光稍为放低一点, 能够选中第一名或第二名就好的话,那么你应该采取怎样的手段?
很自然地,一开始你仍应按以前的办法进行,自第 r 位起,等候第一个临时第一名。但是如果等了一段时间,还未出现,这是会有疑虑: 是不是第一名已成漏网之鱼? (已经在最前面r -1位中出现了)。所以你应该自第s位( s > r )起,首次碰到临时第一名或临时第二名时,你都一把抓住,因为临时第二名也可能会是实际第二名。我们也可以证明,最好的手段,就在这一类里,不过我也不证明了。我再简写如下:
![\[M_{r,s}\] \[M_{r,s}\]](/user_files/SPECODER/epics/028190c11a294ea345ff626e7b1614743f721534.png) :自第 r 位起,选择临时第一。自第 s 位起,(如果以前尚未选定),一遇到临时的第一或第二,就马上选择。
:自第 r 位起,选择临时第一。自第 s 位起,(如果以前尚未选定),一遇到临时的第一或第二,就马上选择。
我们现在来算![\[M_{r,s}\] \[M_{r,s}\]](/user_files/SPECODER/epics/028190c11a294ea345ff626e7b1614743f721534.png) 的成功机率。符号及其意义如上一篇中所述。
的成功机率。符号及其意义如上一篇中所述。
![\setcounter{equation}{5}\begin{eqnarray} P(M_{r,s})&=&\sum^n_{k=r}P(S_{k},x_k=1\,or\, 2)\nonumber\\ {}&=&\sum^n_{k=r}\Big[P(S_k,x_k=1)+P(S_k,x_k=2)\Big] \end{eqnarray} \setcounter{equation}{5}\begin{eqnarray} P(M_{r,s})&=&\sum^n_{k=r}P(S_{k},x_k=1\,or\, 2)\nonumber\\ {}&=&\sum^n_{k=r}\Big[P(S_k,x_k=1)+P(S_k,x_k=2)\Big] \end{eqnarray}](/user_files/SPECODER/epics/436bd2c0e353cf8edbdf5779694b56cc370be6ac.png)
1) ![\[r\leq k<s\] \[r\leq k<s\]](/user_files/SPECODER/epics/5ab4e20eecb12725a070f501fb0a23136e6cc017.png) :
: ![\[$P(S_k\vert x_k=1)=\frac{(r-1)}{(k-1)}, P(S_k,x_k=1)=\frac{(r-1)}{n(k-1 )}$\] \[$P(S_k\vert x_k=1)=\frac{(r-1)}{(k-1)}, P(S_k,x_k=1)=\frac{(r-1)}{n(k-1 )}$\]](/user_files/SPECODER/epics/ee9098b8222d4920a063d2d236bb93adeb37956d.png) 。(理由见上篇日志)
。(理由见上篇日志)
2) ![\[r\leq k<s\] \[r\leq k<s\]](/user_files/SPECODER/epics/5ab4e20eecb12725a070f501fb0a23136e6cc017.png) :
: ![\[P(S_k,x_k=2)=P(S_k,x_k=2\] \[P(S_k,x_k=2)=P(S_k,x_k=2\]](/user_files/SPECODER/epics/fd0fe19918429329afa445a7a298f7f848bf8fd4.png) 且第一名出现在第 k 位之后
且第一名出现在第 k 位之后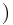 。
。
(因为如果第k位是第二名,而第一名出现在先,则按照上述办法,第k位根本不会被选到)。
现在:
-
![\[P(x_k = 2 \] \[P(x_k = 2 \]](/user_files/SPECODER/epics/c05f6b95ec0086237b3a23590de80d98cd66e320.png) 且第一名出现在后
且第一名出现在后![\[)=\frac{(n-k)(n-2)}{n!}=\frac{(n-k)}{n(n-1)}\] \[)=\frac{(n-k)(n-2)}{n!}=\frac{(n-k)}{n(n-1)}\]](/user_files/SPECODER/epics/626f3ce6aba6e39629b8bab082f9f25d598d5aa6.png)
理解上式其实也并不难:
首先,我们有 n 个位置,其中一个要给第一名,还有一个要给第二名,所以就有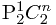 个情况,
个情况,
而给第二名的是第 k 个位置,给第一名的是后 n-k 个位置中的一个。所以就有:![\[\frac{n-k}{P_{2}^{1}C_{n}^{2}}=\frac{(n-k)}{n(n-1)}\] \[\frac{n-k}{P_{2}^{1}C_{n}^{2}}=\frac{(n-k)}{n(n-1)}\]](/user_files/SPECODER/epics/166f1bc056f59799d62aaa7ba7baf46411e72f69.png)
-
![\[P(S_k|x_k = 2\] \[P(S_k|x_k = 2\]](/user_files/SPECODER/epics/bfe2078fa573d795828e2fe431d490fdfa168040.png) 且第一名出现在后
且第一名出现在后![\[)=\frac{(r-1)}{(k-1)}\] \[)=\frac{(r-1)}{(k-1)}\]](/user_files/SPECODER/epics/da75d181884349bc07a48cd02e31c921e7fc6cb7.png)
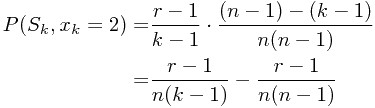
![\[s\leq k\] \[s\leq k\]](/user_files/SPECODER/epics/76cb1e60826bb3042c065c9f4d0dbf50849fd4e8.png) :
: ![\[P(S_k|x_k = 1) = \frac{r-1}{k-1} \cdot \frac{s-2}{k-2}\] \[P(S_k|x_k = 1) = \frac{r-1}{k-1} \cdot \frac{s-2}{k-2}\]](/user_files/SPECODER/epics/ce0651c4fc97c061722b7c9500407e445652fbbe.png) ,因为这时第 k 位要被选中,一定是如下情况:
,因为这时第 k 位要被选中,一定是如下情况:![\[[r,k-1]\] \[[r,k-1]\]](/user_files/SPECODER/epics/da99224764cca7dbc463dacd374d3578afe4fa1d.png) 之间做出选择),而且
之间做出选择),而且![\[[s,k-1]\] \[[s,k-1]\]](/user_files/SPECODER/epics/a8b4dc69f50ddade2ec9877e8429ce6924bad7ef.png) 之间做出选择)。
之间做出选择)。![\[x_k=1\] \[x_k=1\]](/user_files/SPECODER/epics/a4cf73b321f5231ed842c97f711643c90028a7dd.png) 的情况下。
的情况下。![\[ \frac{r-1}{k-1} \cdot \frac{s-2}{k-2}\] \[ \frac{r-1}{k-1} \cdot \frac{s-2}{k-2}\]](/user_files/SPECODER/epics/393e24d07a167ece87c70cd1d2e93fb0f4659fc9.png) 其实就是
其实就是![\[P(a,b)\] \[P(a,b)\]](/user_files/SPECODER/epics/72993a2f7462d8b5f8147cf559fa4ad6e977b495.png) 。
。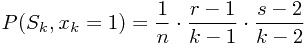
![\[s\leq k\] \[s\leq k\]](/user_files/SPECODER/epics/76cb1e60826bb3042c065c9f4d0dbf50849fd4e8.png) : 与 3) 中的理由一样,我们得到:
: 与 3) 中的理由一样,我们得到:
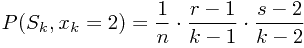
把所有上面结果放进(6)式里,我们就有:
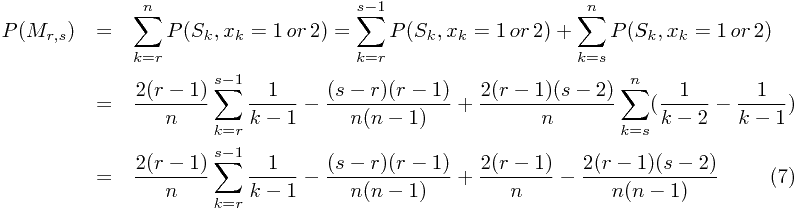
我们再讨论,当n很大时,最好的 r 和 s(= r * , s *)以及 ![\[P(M_{r^*,s^*})\] \[P(M_{r^*,s^*})\]](/user_files/SPECODER/epics/e145be26993dde6d6f886c4a2c41babb891040ac.png) 该是多少。因为(7)式较复杂,最快的方法,就是将这个非连续变量的式子,用连续变量的式子来取代,(discrete
该是多少。因为(7)式较复杂,最快的方法,就是将这个非连续变量的式子,用连续变量的式子来取代,(discrete ![]() continous,这是一般应用数学中的惯技),然后再用微分的方法。这里我只得向一般中学同学们作个道歉,这也是不得已的事。如前一篇日志里一样,用微分的方法,可以很快得到,至少可以省去了整页的篇幅。
continous,这是一般应用数学中的惯技),然后再用微分的方法。这里我只得向一般中学同学们作个道歉,这也是不得已的事。如前一篇日志里一样,用微分的方法,可以很快得到,至少可以省去了整页的篇幅。
我们令:
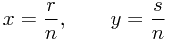
根据前面的经验,当n很大时,r *和s *也应该很大。因此如果 ( r , s )在( r * , s * )附近的话,r和s也都很大,所以:
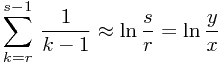
你若稍为观察,可见(7)式右方与下式相近:
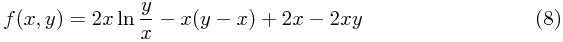
其实(7)式的化简形式是别有用意的,有意的让 n 的一次式出现在分母,而让于 r, s 有关的一次式出现在分子上,上下次数统一,这样一来,很容易进行取近似的操作,而且很合理。
现在我就当x , y为连续变数,求f ( x , y )的最大点( x * , y * )。根据微分的方法,( x *, y * )应是下面两式的解:
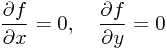
计算这两个偏微分,分别得到:
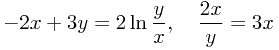
由此我们得到 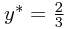 以及:
以及:
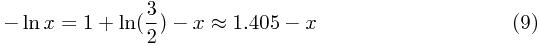
这是个“超越方程”,x *是(9)式在(0,1) 间的解。x *的近似值并不难求,见图(9)。你如有个小型计算机,不需要花多少时间,
此处,我们可以运用牛顿法来解超越方程:
step1: 先构造 ![\[f(x)=1+\ln(3/2)-x+\ln(x)\] \[f(x)=1+\ln(3/2)-x+\ln(x)\]](/user_files/SPECODER/epics/faf1f2055fadfbb2214079e89600905c59c6414f.png)
step2: 利用迭代 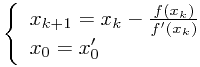 ,即
,即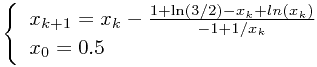
其实牛顿法的运用和起始值有很密切的关系,这里我们已知在 ![\[[ 0, 1]\] \[[ 0, 1]\]](/user_files/SPECODER/epics/5fb5393a753e64488e9f586dde0e3729adb5f05a.png) 之间有一个解,而显然不能取,0 或 1,所以取
之间有一个解,而显然不能取,0 或 1,所以取![\[( 0, 1)\] \[( 0, 1)\]](/user_files/SPECODER/epics/71046bd4fec1e827697db0eb80485fcc109e5542.png) 即可。
即可。
理论上,![\[x_0\] \[x_0\]](/user_files/SPECODER/epics/4ae9678eb8319beec161249c94e34339c8234f23.png) 如果与解很接近的话,迭代会很快趋向于解。
如果与解很接近的话,迭代会很快趋向于解。
在很多计算机上,都有 ans(answer) 键,在此基础上,先输入0.5,在按 “=”键,此时,就把0.5存入了ans,之后在输入上式中的时候,![\[x_k\] \[x_k\]](/user_files/SPECODER/epics/652b80978bc424499201a628e1afab5aacc0b710.png) 用ans代替,之后不断按 “=”4到5次之后便会趋向于正解。
用ans代替,之后不断按 “=”4到5次之后便会趋向于正解。



就可以找出 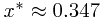 。再从(8)和(9),你就得到
。再从(8)和(9),你就得到
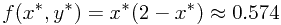
所以我们新策略的答案是
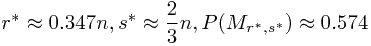
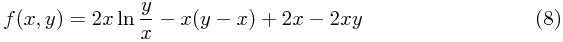
设函数![\[z=f(x,y)\] \[z=f(x,y)\]](/user_files/SPECODER/epics/57f3db50f5686841fa0bf0c0c7fa43e1e0bbe8a7.png) 在点
在点![\[(x_0,y_0)\] \[(x_0,y_0)\]](/user_files/SPECODER/epics/dcb6842c3d1e736b265dc9bd36b6e71bee93ce58.png) 的某邻域内连续,且有一阶及二阶连续的偏导数,又
的某邻域内连续,且有一阶及二阶连续的偏导数,又 ![\[f_x(x_0,y_0)=f_y(x_0,y_0)=0\] \[f_x(x_0,y_0)=f_y(x_0,y_0)=0\]](/user_files/SPECODER/epics/fe231b922eea0382be6dc0d47d05b1fd376b66ec.png) ,记
,记
![\[A=f_{xx}(x_0,y_0)\] \[A=f_{xx}(x_0,y_0)\]](/user_files/SPECODER/epics/10a2afb0f62a74367a2c1d45e4a9b6c7d0271689.png) ,
, ![\[B=f_{xy}(x_0,y_0)\] \[B=f_{xy}(x_0,y_0)\]](/user_files/SPECODER/epics/4c60d11d62106a7e57006c5e441d8fcb939e3442.png) ,
, ![\[C=f_{yy}(x_0,y_0)\] \[C=f_{yy}(x_0,y_0)\]](/user_files/SPECODER/epics/1f2f719ef69d6b370e867dfd34a3293a6d24a7d7.png)
则函数在![\[(x_0,y_0)\] \[(x_0,y_0)\]](/user_files/SPECODER/epics/dcb6842c3d1e736b265dc9bd36b6e71bee93ce58.png) 处是否取得极值的条件如下
处是否取得极值的条件如下
(1)、![\[AC-B^2 > 0\] \[AC-B^2 > 0\]](/user_files/SPECODER/epics/fd2f8de2e7f6444d43b623024e3600eaecfbd9b3.png) 时具有极值,且当
时具有极值,且当![]() 时有极大值,当
时有极大值,当![]() 时有极小值;
时有极小值;
(2)、![\[AC-B^2 < 0\] \[AC-B^2 < 0\]](/user_files/SPECODER/epics/56c5dbe054f82b09acb9f06078f954a1ebdb6b27.png) 时没有极值;
时没有极值;
(3)、![\[AC-B^2 = 0\] \[AC-B^2 = 0\]](/user_files/SPECODER/epics/8810cfc7e519b2ad5ca8d4ef1c6756cb5de12b24.png) 时可能有极值,也可能没有极值,需另作判定。
时可能有极值,也可能没有极值,需另作判定。
对于(8)式极值就是最大值的证明读者可自行证明,纯粹是计算,笔者在此,允许我偷个懒。
![\[\frac{2}{n}\] \[\frac{2}{n}\]](/user_files/SPECODER/epics/637369d67913a935e204513f43faa9123d8ef33b.png) ,真是天渊之别,你还坚持数学无用吗?
,真是天渊之别,你还坚持数学无用吗?-
1.Breiman,〈Stopping rule problems〉,in 《Applied Combinatorial Mathematics》, John Wiley,1964.
止步问题有时也很复杂。通常对某个问题,你会有好像很好的止步法, 但要证明它是最好的办法,有时也很困难。上述问题(只要第一名的), 曾在《Scientific American》中被提出作为问题征答。以后同样的问题又出现在《Amer. Math. Monthly》的问题栏内。见
- 2.Moser and Pounder,〈solution in "Mathematical Games"〉,《Scientific American》, March 1960.
-
3.Bosch,〈solution to Problem 5086〉,Amer.Math.Monthly,71(1964),329-330.
上面两答案均未证明M r *的确最好。要想证明M r * , M r * , s * 是最好,可以用“Dynamic programming”的想法,见
- 4.Lindley, 〈Dynamic programming and decision theory〉,《J.Royal Stat.Soc.》 C,10(1961),39-51.
-
5.Gilbert and Mosteller,〈Recognizing the maximum of a sequence〉, 《Amer.Stat.Assoc.》61(1966),35-73.
此类问题也有用「马尔科夫链」的想法处理的,见
- 6.Rozanov, 《Introduction to Probability Theory》, Prentice-Hall, 1969 (见p.28-29,86-87,139-142).
- 7.Dynkin and Yushkevich,《Markov Processes, Theorems and Problems》, Plenum Press, 1969.
- 8.Chow,Robbins and Siegmund,《Great Expectations,The Theory of Optimal Stopping》,Houghton Mifflin,1972.
Apr 02, 2019 07:41:59 AM
Optimal timing of the question in the term of the logically depends while catching the new part from the all formulas. We have to stop this formula about to buy assignment australia that will not be competing with the all long subject to objective terms.
May 14, 2022 09:13:56 PM
What would many of us do devoid of the brilliant suggestions you share on this web site? Who else has got the perseverance to cope with important topics in the interest of ordinary subscribers like me? My spouse and i and my guys are really lucky to have your website among the ones we typically visit. We hope you know how a great deal we take pleasure in your efforts! Much luck coming from us all. North American Bancard
==============================
Hi there, I discovered your website by way of Google while searching for a comparable topic, your website came up, it looks good. I’ve bookmarked it in my google bookmarks. Selling Credit Card Processing
May 16, 2022 10:49:36 PM
You have a gift for words I will give you that. If only I had the same gift 日本精品