SRM 144 DIV 2 1100
调和级数与欧拉常数
形如：![\[\sum_{i=1}^{n}\frac{1}{i}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\]](/user_files/SPECODER/epics/d744f05e5e7bd84791b946a013611a4731f16a35.png "\[\sum_{i=1}^{n}\frac{1}{i}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\]")
的级数称作调和级数。
数百年前，数学家们就对其极限长生了兴趣：
即：![\[\lim_{n\rightarrow+\infty}\sum_{i=1}^{n}\frac{1}{i}\]](/user_files/SPECODER/epics/aa3eeddf1fda7fa922a007b04bc0cf8f758de51a.png "\[\lim_{n\rightarrow+\infty}\sum_{i=1}^{n}\frac{1}{i}\]")
是否存在。（n ,i 均为自然数）
下面给出最简单也是最显而易见的证明：
最佳止步问题（optimal stopping）[3]
退而求其次:
如果你把眼光稍为放低一点， 能够选中第一名或第二名就好的话，那么你应该采取怎样的手段?
很自然地，一开始你仍应按以前的办法进行，自第 r 位起，等候第一个临时第一名。但是如果等了一段时间，还未出现，这是会有疑虑: 是不是第一名已成漏网之鱼? (已经在最前面r -1位中出现了)。所以你应该自第s位( s > r )起，首次碰到临时第一名或临时第二名时，你都一把抓住，因为临时第二名也可能会是实际第二名。我们也可以证明，最好的手段，就在这一类里，不过我也不证明了。我再简写如下：
最佳止步问题（optimal stopping）[2]
最佳的选择：
首先我们先规定几个标记，以方便论证：
![\[x_{k}\]](/user_files/SPECODER/epics/0318b5382a48a5052b3125eea904dac342fb5c59.png "\[x_{k}\]")
:表示第 k 个物品的名次，即实际名次。显然，这是个随见变量，而且我们对于该名次，之前是一无所知的，但是我们知道的，是每个物品的临时名次，也就是说，当我们看到第 k 个物品时，该物品在前 k 个物品中排第几我们是知道的。
前面简单的办法，即放弃前面一半，结果已经十分不错了，我们自然会想到跟一般的办法。
最佳止步问题（optimal stopping）[1]
首先让我们看一个问题：
You are observing a sequence of objects which can be ranked from best to worst. You wish to choose a stopping rule which maximises your chance of picking the best object.
Here, if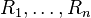 
(n is some large number, perhaps) are the ranks of the objects, and yi is the chance you pick the best object if you stop intentionally rejecting objects at step i, then (Ri) and (yi) are the sequences associated with this problem.